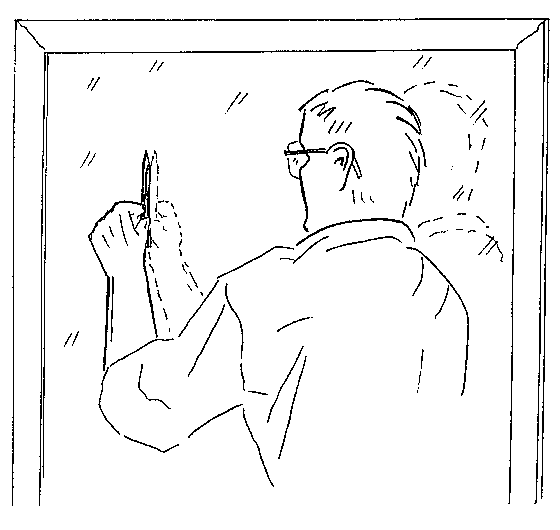
Reprinted from Optics and Photonics News / January 1995 / pp. 42,43:   EVERYDAY OPTICS We live surrounded by plane mirrors on walls, doors, and vending machines. We have repeatedly heard explanations of the reversed "handedness" of the mirror images we see.  Yet, I have not heard any mention of a striking mirror image illusion that is easily observed in most homes.  To see it, place one ear firmly against a common household mirror and look at a pencil held flat against the mirror some 30-40 cm in front of you.  The pencil point and its mirror image are both clearly visible, but the mirror image appears to be 1 cm (or more) closer to you than the object itself! (Fig. 1.) Figure 1.  Place a pencil, held with its point upward. against a common glass mirror. View it with your head pressed against the mirror and your eyes 30 or 40 cm from the pencil. The mirror image will, surprisingly, appear closer than the pencil Itself. (picture)             What has happened to the conventional wisdom about plane mirror images, and even about symmetry?  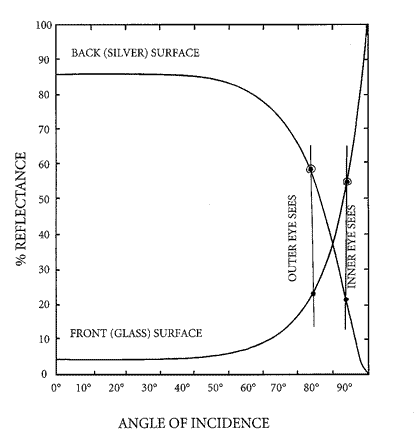A full explanation brings in elements of geometrical, physical, and perceptual optics, and may be an excellent classroom exercise.             A common door-mounted glass mirror is 5-6 mm thick.  At small angles of incidence, the silver backing has a reflectance of about 94%, and the glass itself reflects about 4.4% at the front surface.  The direct frontal view includes the primary image of about 86% (after the back reflection and two transmissions through the front), but also the 4.4% surface reflection, and a series of progressively dimmer multiple reflections.  When viewed from an oblique angle, the silver reflectance stays at about 94%, but the front-surface reflectance rises with angle in an accelerating way (that we can calculate from the Fresnel reflection coefficients for a dielectric interface), so most of the reflection at really oblique angles is from the front surface of the glass -- very little of the light even reaching the silver on the back (Fig. 2). Figure 2. Reflectance of both the front-surface and back-surface images from a glass mirror, as a function of angle of incidence. These were calculated from the Fresnel reflection coefficients for the glass surface, with the two possible polarizations averaged together as the last step. Vertical lines pair the dominant and secondary image seen by each eye in the viewing geometry described in Figure 3. (picture)             The transition between back- and front-surface dominant reflections can be seen in a simpler observation.  When you press your forehead against a door-mounted mirror and view your toes, most of the image comes from the glass surface; at intermediate heights you see a progressive change between the visibility of the silver image and of the surface ghost, or vice versa. For me, the two are balanced in viewing a finger or a pencil held against the glass a little above waist level.             In the new illusion described here, the eye closer to the mirror sees mostly the glass surface reflection image of the pencil, but the outer eye sees mostly the silver image.  At an optimum distance the stronger image for each eye is more than 2.5 times as visible as the respective ghost image, and the stronger image at each eye decisively dominates in the binocular perception of the location of the pencil.             For a model to caculate, I have taken the pencil diameter as 8 mm, the mirror thickness as 5.5 mm, the refractive index as 1.53, and the eye distances from the mirror surface as 35 mm and 100 mm. With these values the best reflectance ratio achievable for both eyes at once is 2.5115, at 35.496 cm distance from the pencil to the eyes, and the binocular mirror image then appears to be 13.92 mm closer than the object itself. (Scaled in Fig. 3.)   Figure 3. Detailed viewing geometry for the binocular oblique view of the pencil in contact with the mirror. The two eyes (out of the illustration to the right) see the pencil image by the dominant reflected rays DE and GH. 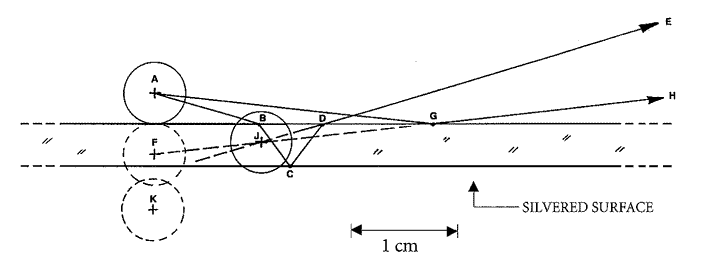(picture)             In Figure 3, the real pencil is placed against the mirror at A.  The image at K is where the pencil will appear to be if seen in the silver back-reflection by both eyes in a conventional (direct) view, and F is its usually dimmer reflection in the glass surface.  Under the conditions of our illusion, the path actually taken by most of the light toward the outer eye is ABCDE. But the eye closer to the mirror receives most of its light from the pencil along the glass-surface reflection, AGH.  The two rays DE and GH, each highly dominant at the respective eye, intersect at (and therefore both appear to originate from) J, so that is where your binocular vision places the apparent reflected image of the pencil.  Notice that the mirror image of the pencil amazingly seems to protrude from the mirror surface, a prediction easily confirmed if you touch it! A discussion of this point may enrich the familiar distinction between real and virtual images.   Acknowledgments I wish to thank J. Bareau and M. Fulton for confirming this observation for me, and for pointing out that when the effect is viewed by two individuals, using one mirror and each observing the same pencil from opposite directions, the reflected image appears to be closer to both of them. ________________________________________________________________________________ William T. Plummer is director of optical engineering at Polaroid Corp., Cambridge, Mass.